문자형 데이터 표현
코드 -> 기계어 : 인코딩
기계어 -> 코드 : 디코딩
통신
- 다른 컴퓨터와 데이터 교환
- CPU가 다른 기기와 데이터 교환
문자
- 숫자, 알파벳 문자, 특수문자로 구성된 집합의 한 원소
- 컴퓨터 시스템마다 문자 집합은 서로 다르며, 여러개 합쳐진 문자를 문자열이라고 함
- 문자가 기억 장소에 저장되는 단위 : Byte(1byte 당 1문자씩, 한글은 2byte 당 1문자)
문자형 데이터 표현
- 영문자(대문자 + 소문자) 52자, 숫자 10자, 한글 2350, 한자 4880자, 특수문자 등 기타 문자 830로 표현
- 정보를 표현 하기 위한 기호 체계 -> 코드(code)
BCD 코드
- 10진수 1자리의 수 를 2진수 4Bit로 표현
- 4Bit의 2진수 각 Bit가 8,4,2,1의 자리 값을 가지므로 8421 코드라고도 한다
- 대중적인 가중치 코드
- 문자 코드인 BCD에서 Zone 부분을 생략한 형태
- 10진수 입출력이 간편
- 예시
- 10진수 125를 BCD코드로 표현
- 1 -> 0001
- 2 -> 0010
- 5 -> 0101
- 125 -> 0001 0010 0101
표준 BCD 코드
- 숫자 코드인 BCD 코드에 2개의 zone bit를 확장한 문자코드
- 컴퓨터에서 문자,숫자,특수 문자 등을 4bit로 표현하기에는 부족 -> BCD코드에 존 비트를 확장한것
- 6개의 데이터 비트와 1개의 체크비트로 구성

- 6개의 Bit로 문자를 표현하는 종류는 총 64가지
- Parity bit : 데이터의 오류를 확인하는 체크비트
- Zone bit : 문자의 그룹을 표시
- Digit bit : BCD로 표시하는 숫자 비트

EBCDIC 코드
- 표준 BCD 코드로 문자를 표현할 경우 단지 64가지의 문자만 표현하는 단점을 오늘날 대분분의 컴퓨팅 시스템에서 사용하는 코드
- 8bit 코드이므로 256가지의 문자와 숫자 등의 데이터를 표현

- 예시
- 17=> 1111000111110111
- 1 => 11 11 0001
- 7 => 11 11 0111
- K9 => 1101000111111001
- K => 11 01 0001
- 9 => 11 11 1001
- 17=> 1111000111110111
ASCII 코드
- 7Bit 코드로 미국표준협회에서 개발
- 1개의 문자를 3개의 Zone Bit와 4개의 Digit Bit로 표현
- 128가지의 문자를 표현
- 각 시스템간의 코드 불일치로 발생하는 문제점들을 방지하기 위해서 제정
- 통신 제어용 및 마이크로컴퓨터의 기본 코드로 사용
- 비가중치 코드

Excess - 3 코드 ( 3초과 코드 )
- BCD + 3, 즉 BCD코드에 3을 더하여 만든 코드
- 모든 비트가 동시에 0이 되는 경우가 없다.
- 대표적인 자기보수 코드
- 끊어 읽기 잘못하는 것을 막기 위한것
- 0000이 초기화 코드여서 이걸 막기 위함
- 비가중치코드
- 예
- 10진수 6을 Excess-3코드로 표현
- 6을 BCD => 0110
- BCD에 3을 더함 => 0110 + 0011 => 1001
자기 보수 (Self Complementing) 코드
- 2진수로 된 코드의 1을 0으로 0을 1로 모두 바꿈으로써 해당 코드의 10진 값에 9의 보수를 얻는 코드
- 예)
- 10진수 5를 4자리 2진수로 변경한 다음 3을 더한다 0101 + 0011 -> 1000
- 코드를 0을 1로 1은 0으로 변경하여 1의 보수를 구한다 1000 -> 0111
- 1의 보수에서 3을 뺸다 0111 - 0011 -> 0100
- 10진수로 변경하면 4이다
Gray 코드
- BCD 코드의 인접하는 Bit를 XOR 연산하여 만든 코드
- 이웃하는 코드가 한 비트만 다르기 때문에 코드 변환이 용이
- I/O, A/D변환기, 주변장치 등에서 숫자를 표현할 때 사용(0~9 까지만 가능)
- 1Bit만 변환시켜 다음 수치로 증가시키기 때문에 하드웨어적인 오류가 적다
- 2진수를 Gray 코드로 변환하는 방법
- 첫 번째 Gray bit는 2진수 bit를 그대로 내려쓴다.
- 두 번째 Gray bit부터는 변경할 2진수의 해당 번째 비트와 그 왼쪽의 비트를 XOR연산하여 쓴다
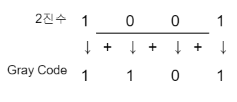
- Gray 코드를 2진수로 변환하는 방법
- 첫 번째 2진수 비트는 Gray bit를 그대로 내려쓴다
- 두 번째 2진수 비트부터는 왼쪽에 구해 놓은 2진수 비트와 변경할 Gray 코드의 해당 번째 비트를 XOR 연산하여 쓴다

7-> 8로 바뀌는 경우에기본은 4bit 모두 바뀌는데 gray code는 1개만 바뀌면 되어서 오류 확률이 적어짐
Parity 검사 코드
- 전송된 코드의 오류를 검사하기 위해서 데이터 비트 외에 1bit의 패리티 체크 비트를 추가
- 1bit의 오류만 검출할 수 있음
- 1개의 개수에 따라 짝수(Even) 패리티와 홀수(Odd) 패리티 방법이 있음
- Odd Parity
- 코드에서 1인 비트의 수가 홀수가 되돌고 0이나 1을 추가
- 예)
- 10100001과 11100010에 홀수 패리티를 추가
- 10100001 -> 101000010 <- 1의 개수가 홀수이므로 0을 추가
- 11100010 -> 111000101 <- 1의 개수가 짝수이므로 1을 추가
- Even Parity
- 코드에서 1인 비트의 수가 짝수가 되도록 0이나 1을 추가
- 예)
- 10100001과 11100010에 짝수 패리티를 추가
- 10100001 -> 101000011 <- 1의 개수가 홀수이므로 1을 추가
- 11100010 -> 111000100 <- 1의 개수가 짝수이므로 0을 추가
해밍 코드
- 오류를 스스로 검출하여 교정이 가능한 코드
- 2bit의 오류를 검출할 수 있고, 1bit의 오류를 교정할 수 있다
- 데이터 비트 외의 오류 검출 및 교정을 위한 잉여 비트가 많이 필요함
- 해밍 코드 중 1,2,4,8,16,...,2^n 번째는 오류 검출을 위한 패리티 비트
- 오류 검출을 위한 패리티비트
- N번째의 패리티 비트는 n번째 비트에서 시작하여 n개의 비트를 포함하고, n개의 비트를 건너편 비트를 대상으로 패리트 비트를 결정
- 1번 패리티 비트를 결정하기 위해서는 1번 비트에서 시작하여 한 비트를 포함하고 한 비트씩 건너뛴 1,3,5,7... 비트가 대상
- 2번 패리티 비트를 결정하기 위해서는 2번 비트에서 시작하여 2 비트를 포함하고 2 비트씩 건너뛴 2,3,6,7... 비트가 대상
- 4번 패리티 비트를 결정하귀 위해서는 4번 비트에서 시작하여 4비트를 포함하고 4비트씩 건너뛴 4,5,6,7,... 비트가 대상
- 문제 예시



