나이브 베이즈 : classifier는 확률적 분류기 계열에 속함
모든 클래스에 대한 확률분포를 예측하기 위해, 각 클래스에 속하는 데이터의 예측 특징
속성이 각각 독립적이다 라고 전제하에
Bayers: bayes' theorem 조건부 확률을 관찬할 특징이 어떤 클래스에 속할지에 대한 조건부 확률에 매핑함
Support Vector Machine
- 선형이나 비선형 분류, 회귀, 이상치 탐색에도 사용할수 있는 다목적 머신러닝 모델
- 고차원 공간에서나 차원 수가 샘플 수보다 많을 때 효과적임 : 고차원 데이터에 효과적인
- SVM은 서로 다른 클래스의 관측값을 가장 잘 분리할 수 있는 최적의 초평면을 찾음
- 초편면은 n 차원의 관측값 특징 공간을 두 개의 공간으로 분리하는 n-1 차원의 평면임
- ㅊ최적의 초평면은 초평면과 이 초평면이 분리하는 두 공간에 있는 가장 가까운 점과 거리가 최대가 되도록 선택

- Separating hyperplane (분리초평면)
- 초평면상의 모든 데이터 포인트 x는
- 궁국적인 모적은 w와 b를 찾는 것!
- 하지만 w와 b에 대해서 가능한 솔루션은 무수히 많음
- 여러가지 가능한 분리 초평면 중에서 가장 적합한 초평면은 어떻게 판별할까?
- 마진을 최대화 -> 에러를 최소화
- Margin은 w
- 초평면과 평행한 것중
- 양수쪽에 있는 평면은 Positive hyperplane
- 음수쪽에 있는 평면은 Negative hyperplane
- y가 -1, 1에 해당하는

Vector norm || W ||p for p = 1,2,3,...
|| W ||p = (시그마 |Wi|p) ^1/p
L2 norm 은 각 요소들을 제곱해서 다 합해준 다음 제곱근을 쓰워준거
L1 norm 은 각 요소들의 절대값의 합의 제곱근
Margin의 거리 = +plane와 -plane의 평행이동한 거리 결국 평면이니까 어쩌구 저쩌구
Margin = 2/L2 norm 을 최대화 하는 것이 목적 -> L2 norm 을 최소화 하는것
Objective : minimize 1/2 * (L2 norm)^2
Subject to 𝑦𝑖 𝑤𝑇 𝑥𝑖 + 𝑏 ≥ 1, 𝑖 = 1,2, … , 𝑛 , 제약식 : Margin >= 1
선형 분류 : Linear SVM ( Hard Margin SVM ) 마진안에는 데이터가 없음
∥ 𝑤𝑥′ + 𝑏 ∥는 데이터 포인트 x와 decision hyperplane 간의 거리로 볼 수 있는데. 이는 예측의 신뢰도라고 해석할 수 있음
이 값이 클수록 데이터 포인트가 결정 경계에서 더 멀리 떨어져 있으므로 예측 확실성이 높아짐
선형으로 는 분류 할 수 없는 경우
- linearly noneseparable case (soft amrgine SVM)
- Misclassification(오분류)를허용하고, 이에 따른 오류를 최소화
- 에러에 관한것
- 𝜉 : 에러에서 각 초평면 까지의 거리
- Objective :
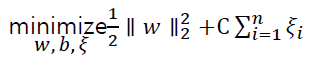
C는 margin과 training error에 대한 trade-off를 결정하는 tuning parameter
C값이 큰 경우 : 오분류에 대한 penalty가 상대적으로 높아짐 -> 오분류를 허락X
C값이 작은 경우 : 오분류에 대한 penalty가 상대적으로 적음 -> 오분류 허락


커널 함수(kernel function)
- 차원이 높아지면 상대적으로 분류가 쉬워질 수도 있음 (아닐수도 있음)
- SVM을 original space가 아닌 feature space에서 학습
- Original space에서 nonlinear decision boundary는 feature space에서 linear decision boundary
- 고차원 feature space 에서는 관측치 분류가 더 쉬울 수 있음
- 어떠한 커널 함수가 좋은지는 노가다(이게 맞음?)
- 종류




Gaussian kernel (Radial basis function (RBF) kernel) 이게 사용 많이 됨 : 사전 정보가 없는 경우에
SVM은 결과에 대한 해석이 어려움 : 근거가 뭐인지 알 수 없음